CIMMiner
CIMMiner generates color-coded Clustered Image Maps (CIMs) ("heat maps") to represent "high-dimensional" data sets such as gene expression profiles. We introduced CIMs in the mid-1990's for data on drug activity, target expression, gene expression, and proteomic profiles. Clustering of the axes brings like together with like to create patterns of color. ( Weinstein, et al., Science 1997; 275:343-349).
-
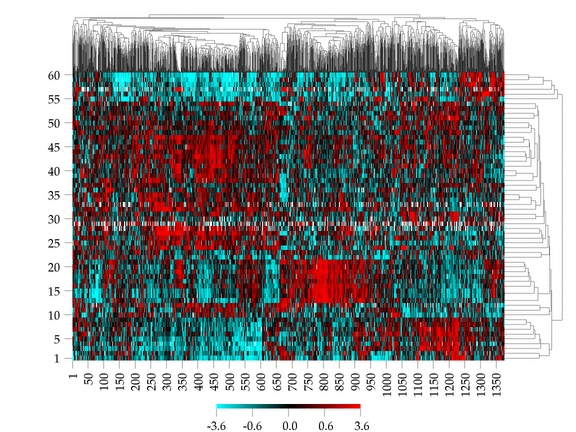
The Clustered Image Map is a 2-dimensional visualization of a real-valued matrix with N rows and M columns (NxM). The CIM has the same number of rows and columns as the matrix and the color at the ith row and jth column is indicative of the corresponding element of the matrix.
Optionally, the rows and/or columns of the matrix can be clustered to identify interesting patterns. This clustering can be done according to several different distance measures and clustering methods.
The above image is an example of genes x cells.
-
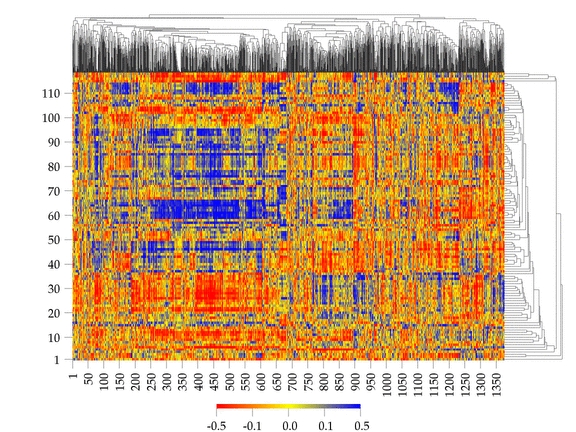
Two matrices are used as input in this case, one NxP and another PxM. From these, a third matrix (the product matrix) of size NxM is created where element (i,j) is the correlation between the ith row of the first the jth column of the second matrix. A CIM for the product matrix is created which is colored according to the elements in the various rows and columns.
The rows and/or columns of the product matrix can be clustered to bring out patterns, but here the clustering is done based on the rows of the first input matrix and the columns of the second input matrix. The rows are reordered by clustering the rows of the first input matrix and this reordering is used for the product matrix. Similarly the clustering of the columns of the second input matrix gives the reordering of the columns of the product matrix.
The above image is an example of genes x drugs.
-
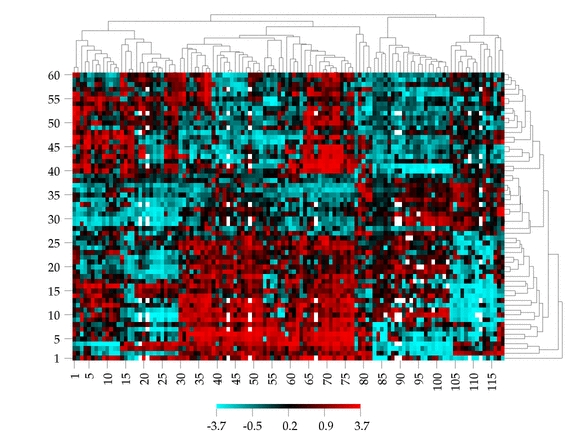
For detailed instruction on how to prepare your dataset and select appropriate distance method and cluster algorithm, please visit our help section.
The above image is an example of drugs x cells.
To learn more details, please check out the following articles.

